คุณสมบัติปริซึม Heptagonal และวิธีการคำนวณปริมาณ

ปริซึม heptagonal เป็นรูปทรงเรขาคณิตที่ชื่อมีความหมายเกี่ยวข้องกับคำจำกัดความทางเรขาคณิตสองประการ ได้แก่ : ปริซึมและ heptagon.

"ปริซึม" เป็นรูปเรขาคณิต จำกัด โดยสองฐานที่เท่ากันและรูปหลายเหลี่ยมขนานและใบหน้าด้านข้างของพวกเขาเป็นรูปสี่เหลี่ยมด้านขนาน.

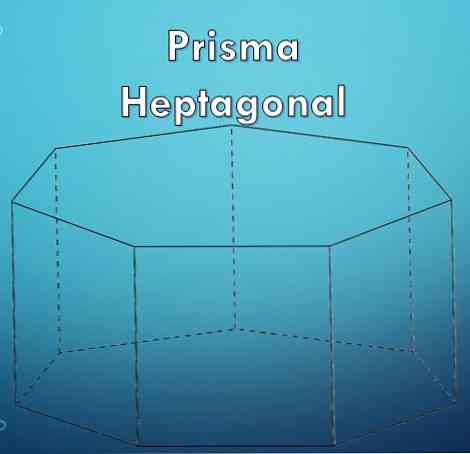
"heptagon" เป็นรูปหลายเหลี่ยมที่เกิดจากเจ็ด (7) ด้าน เนื่องจาก heptagon เป็นรูปหลายเหลี่ยมมันอาจเป็นได้ว่ามันเป็นปกติหรือผิดปกติ.

รูปหลายเหลี่ยมนั้นถือว่าปกติถ้าทุกด้านของมันมีความยาวเท่ากันและมุมภายในของมันวัดเหมือนกันพวกมันจะเรียกว่ารูปหลายเหลี่ยมด้านเท่ากันหมด; ไม่เช่นนั้นจะกล่าวว่ารูปหลายเหลี่ยมนั้นไม่สม่ำเสมอ.

ลักษณะของปริซึม Heptagonal

ต่อไปนี้เป็นคุณสมบัติบางอย่างที่มีปริซึม heptagonal เช่น: การก่อสร้าง, คุณสมบัติของฐาน, พื้นที่ของใบหน้าทั้งหมดและปริมาณ.

1- การก่อสร้าง

เพื่อสร้างปริซึม heptagonal จำเป็นต้องมี heptagons สองอันซึ่งจะเป็นฐานและเจ็ดรูปสี่เหลี่ยมด้านขนานหนึ่งอันในแต่ละด้านของ heptagon.

เริ่มต้นด้วยการวาด heptagon แล้ววาดเส้นแนวตั้งเจ็ดเส้นที่มีความยาวเท่ากันซึ่งมาจากจุดยอดแต่ละจุด.

ในที่สุดก็มีการวาด heptagon อื่นเพื่อให้จุดยอดของมันตรงกับจุดสิ้นสุดของเส้นที่วาดในขั้นตอนก่อนหน้า.

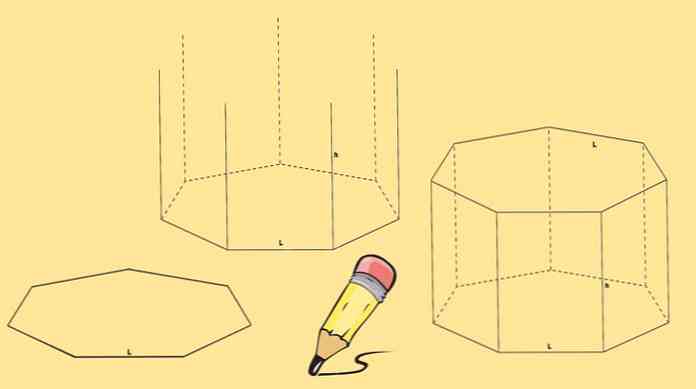
ปริซึม heptagonal ที่ถูกวาดข้างบนเรียกว่าปริซึม heptagonal แต่คุณยังสามารถมีปริซึม heptagonal แบบเอียงได้เช่นเดียวกับในรูปต่อไปนี้.

2- คุณสมบัติของฐาน

เนื่องจากฐานของพวกมันเป็น heptagons พวกมันจึงยอมรับว่าจำนวนเส้นทแยงมุมคือ D = nx (n-3) / 2 โดยที่ "n" คือจำนวนด้านของรูปหลายเหลี่ยม; ในกรณีนี้เรามี D = 7 × 4/2 = 14.

เราสามารถเห็นได้ว่าผลรวมของมุมภายในของ heptagon ใด ๆ (ปกติหรือผิดปกติ) เท่ากับ900º นี้สามารถตรวจสอบได้โดยภาพต่อไปนี้.

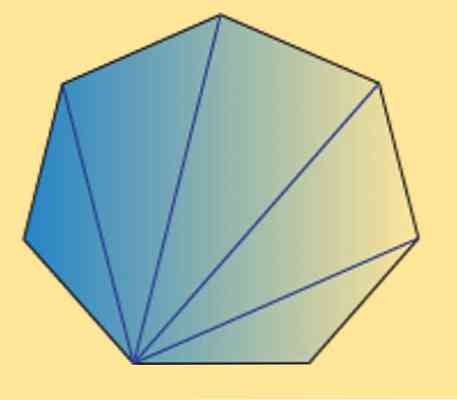
อย่างที่คุณเห็นมีรูปสามเหลี่ยมภายใน 5 รูปและการใช้ผลรวมของมุมภายในของรูปสามเหลี่ยมเท่ากับ 180 can สามารถได้ผลลัพธ์ที่ต้องการ.

3- พื้นที่ที่จำเป็นในการสร้างปริซึม Heptagonal

เนื่องจากฐานของมันมีสอง heptagons และด้านข้างของมันคือเจ็ดสี่เหลี่ยมด้านขนานพื้นที่ที่จำเป็นในการสร้างปริซึม heptagonal เท่ากับ 2xH + 7xP โดยที่ "H" เป็นพื้นที่ของ heptagon แต่ละอันและ "P" ของแต่ละสี่เหลี่ยมด้านขนาน.

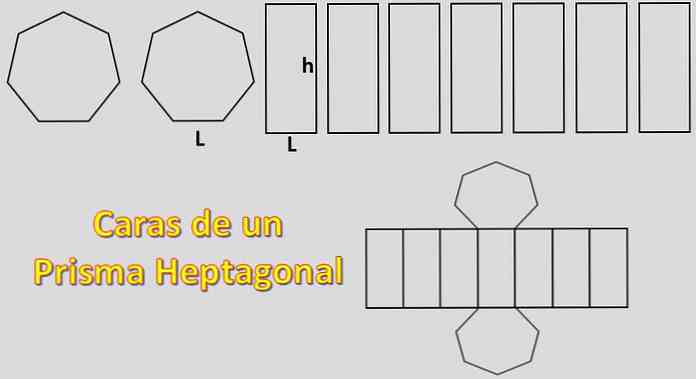
ในกรณีนี้จะคำนวณพื้นที่ของ heptagon ปกติ สำหรับสิ่งนี้เป็นสิ่งสำคัญที่จะต้องรู้คำนิยามของ apothema.

Apothem เป็นเส้นตั้งฉากที่เปลี่ยนจากจุดศูนย์กลางของรูปหลายเหลี่ยมปกติไปจนถึงจุดกึ่งกลางของด้านใดด้านหนึ่ง.

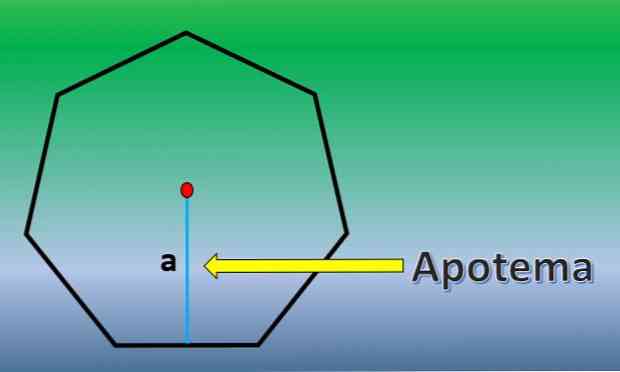
เมื่อทราบถึง Apothem พื้นที่ของ heptagon คือ H = 7xLxa / 2 โดยที่ "L" คือความยาวของแต่ละด้านและ "a" ความยาวของ apothem.

พื้นที่ของรูปสี่เหลี่ยมด้านขนานนั้นง่ายต่อการคำนวณถูกกำหนดเป็น P = Lxh โดยที่ "L" คือความยาวเท่ากันของด้านข้างของ heptagon และ "h" คือความสูงของปริซึม.

โดยสรุปปริมาณของวัสดุที่จำเป็นในการสร้างปริซึม heptagonal (ที่มีฐานปกติ) คือ 7xLxa + 7xLxh นั่นคือ 7xL (a + h).

4- ปริมาณ

เมื่อทราบพื้นที่ของฐานและความสูงของปริซึมปริมาตรจะถูกกำหนดเป็น (พื้นที่ฐาน) x (ความสูง).

ในกรณีของปริซึม heptagonal (ที่มีฐานปกติ) จะมีปริมาณที่ V = 7xLxaxh / 2 สามารถเขียนเป็น V = Pxaxh / 2 โดยที่ "P" คือขอบเขตของ heptagon ปกติ.

การอ้างอิง

1. Billstein, R. , Libeskind, S. , & Lott, J. W. (2013). คณิตศาสตร์: แนวทางการแก้ปัญหาสำหรับครูการศึกษาขั้นพื้นฐาน. López Mateos Editores.
2. Fregoso, R. S. , & Carrera, S. A. (2005). คณิตศาสตร์ 3. บรรณาธิการ Progreso.
3. Gallardo, G. , & Pilar, P. M. (2005). คณิตศาสตร์ 6. บรรณาธิการ Progreso.
4. Gutiérrez, C. T. , & Cisneros, M. P. (2005). หลักสูตรคณิตศาสตร์ 3. บรรณาธิการ Progreso.
5. Kinsey, L. , & Moore, T. E. (2006). สมมาตรรูปร่างและพื้นที่: ความรู้เบื้องต้นเกี่ยวกับคณิตศาสตร์ผ่านเรขาคณิต (ภาพประกอบ, พิมพ์ซ้ำ) Springer Science & Business Media.
6. มิทเชล, C. (1999). การออกแบบเส้นคณิตศาสตร์พราว (ภาพประกอบ ed.) Scholastic Inc.
7. R. , M. P. (2005). ฉันวาด6º. บรรณาธิการ Progreso.