ปริซึมหกเหลี่ยมมีขอบจำนวนเท่าใด
น่ารู้ ปริซึมหกเหลี่ยมมีขอบจำนวนเท่าใด ต้องรู้จักความหมายของ "edge", "ปริซึม" และ "hexagonal" แนวคิดสองข้อแรกเป็นคำจำกัดความทั่วไปและแนวคิดที่สามเกี่ยวข้องกับรูปร่างของรูปทรงเรขาคณิต.
เมื่อพูดถึงหกเหลี่ยมการพูดถึงที่ทำจากรูปหกเหลี่ยม (รูปหลายเหลี่ยม) คำนำหน้า "hexa" ระบุว่ารูปหลายเหลี่ยมมีหกด้าน.

Edge คือขอบของวัตถุ ในทางเรขาคณิตมันเป็นเส้นที่เชื่อมต่อสองจุดยอดต่อเนื่องของรูปทรงเรขาคณิต.
ปริซึมเป็นรูปทรงเรขาคณิตที่ถูก จำกัด ด้วยสองฐานที่ขนานและรูปหลายเหลี่ยมเท่ากันและใบหน้าด้านข้างของพวกเขาคือรูปสี่เหลี่ยมด้านขนาน.
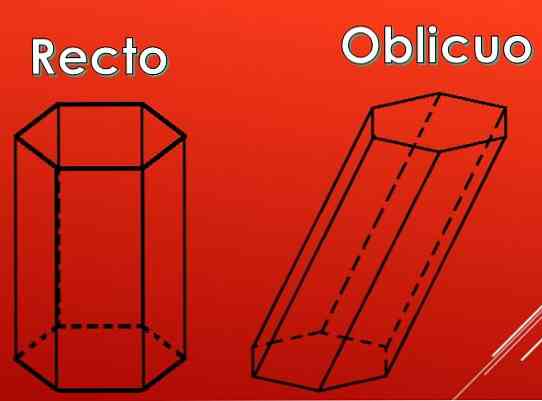
ในภาพต่อไปนี้จะเห็นได้ว่าใบหน้าด้านข้างของปริซึมหกเหลี่ยมสามารถเป็นรูปสี่เหลี่ยมผืนผ้าได้ แต่พวกเขายังสามารถเป็นรูปสี่เหลี่ยมด้านขนาน.
ตามชนิดของรูปสี่เหลี่ยมด้านขนานพรีเมี่ยมสามารถแบ่งออกเป็นสองประเภท: ตรงและเฉียง.
วิธีการนับขอบของปริซึมหกเหลี่ยม?
จำนวนของขอบที่ปริซึมหกเหลี่ยมจะไม่เปลี่ยนแปลงหากเป็นปริซึมตรงหรือเฉียง นอกจากนี้จำนวนขอบไม่ได้ขึ้นอยู่กับความยาวของด้านทั้ง.
การนับขอบของปริซึมหกเหลี่ยมสามารถทำได้หลายวิธี นี่คือสองวิธี:
1- ย่อยปริซึม
วิธีหนึ่งในการนับขอบคือการย่อยสลายปริซึมหกเหลี่ยมในฐานสองฐานและใบหน้าด้านข้าง ด้วยวิธีนี้คุณจะได้รูปหกเหลี่ยมสองรูปและสี่เหลี่ยมด้านขนานที่มีเส้นด้านในห้าเส้น.
หกเหลี่ยมแต่ละอันมีหกขอบดังนั้นปริซึมจะมีมากกว่า 12 ขอบ.
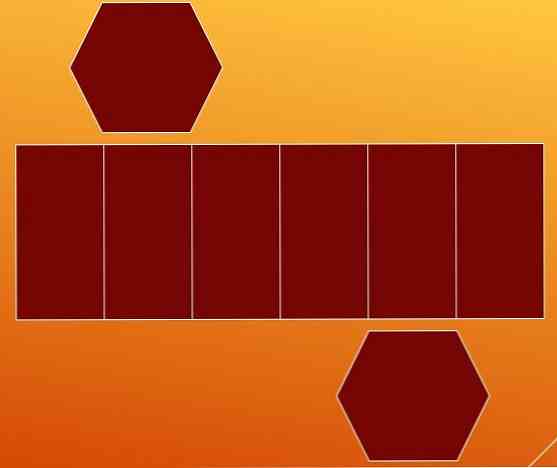
เมื่อมองแวบแรกมันเป็นความคิดที่ว่าสี่เหลี่ยมด้านขนานมีเก้าขอบ (เจ็ดแนวตั้งและแนวนอนสอง) แต่จะสะดวกในการหยุดการวิเคราะห์กรณีนี้.
เมื่อรูปสี่เหลี่ยมด้านขนานงอเป็นรูปแบบของปริซึมจะเห็นได้ว่าบรรทัดแรกทางซ้ายจะรวมกับบรรทัดสุดท้ายทางด้านขวาซึ่งทั้งสองเส้นแสดงขอบเดียว.
แต่สิ่งที่เกี่ยวกับเส้นแนวนอนสองเส้น?
เมื่อชิ้นส่วนทั้งหมดถูกประกอบเข้าด้วยกันอีกครั้งเส้นแนวนอนจะถูกรวมเข้าด้วยกันโดยแต่ละอันจะมีหกขอบของแต่ละรูปหกเหลี่ยม ด้วยเหตุนี้การนับแยกต่างหากจึงเป็นความผิดพลาด.
สี่เหลี่ยมด้านขนานมีหกขอบปริซึมซึ่งรวมกับ 12 ขอบนับที่จุดเริ่มต้นให้รวม 18 ขอบ.
2.- ฉายแต่ละขอบ
อีกวิธีหนึ่งที่ง่ายกว่าในการนับขอบคือการใช้ความจริงที่ว่าฐานของปริซึมหกเหลี่ยมเป็นรูปหกเหลี่ยมแล้วแต่ละฐานมีหกขอบ.
ในอีกด้านหนึ่งจากจุดยอดหกเหลี่ยมแต่ละอันขอบเดี่ยวจะถูกฉายไปที่จุดยอดที่สอดคล้องกันของรูปหกเหลี่ยมอื่น ๆ นั่นคือมีหกขอบที่รวมฐานหนึ่งกับอีก.
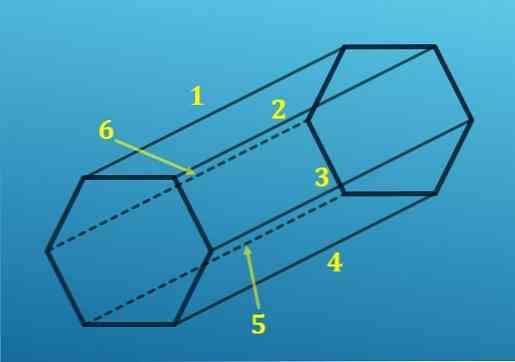
ด้วยการเพิ่มขอบทั้งหมดคุณจะได้รับทั้งหมด 18 เส้น.
ข้อสรุป
สามารถแสดงให้เห็นว่าจำนวนขอบของปริซึมเท่ากับสามเท่าของจำนวนขอบที่รูปหลายเหลี่ยมที่มี.
ดังนั้นปริซึมห้าเหลี่ยมจะมี 3 * 5 = 15 ขอบปริซึมแบบ heptagonal จะมี 3 * 7 = 21 ขอบดังนั้นจึงสามารถใช้กับปริซึมใดก็ได้.
การอ้างอิง
- Billstein, R. , Libeskind, S. , & Lott, J. W. (2013). คณิตศาสตร์: แนวทางการแก้ปัญหาสำหรับครูการศึกษาขั้นพื้นฐาน. López Mateos Editores.
- Fregoso, R. S. , & Carrera, S. A. (2005). คณิตศาสตร์ 3. บรรณาธิการ Progreso.
- Gallardo, G. , & Pilar, P. M. (2005). คณิตศาสตร์ 6. บรรณาธิการ Progreso.
- Gutiérrez, C. T. , & Cisneros, M. P. (2005). หลักสูตรคณิตศาสตร์ 3. บรรณาธิการ Progreso.
- Kinsey, L. , & Moore, T. E. (2006). สมมาตรรูปร่างและพื้นที่: ความรู้เบื้องต้นเกี่ยวกับคณิตศาสตร์ผ่านเรขาคณิต (ภาพประกอบ, พิมพ์ซ้ำ) Springer Science & Business Media.
- มิทเชล, C. (1999). การออกแบบเส้นคณิตศาสตร์พราว (ภาพประกอบ ed.) Scholastic Inc.
- R. , M. P. (2005). ฉันวาด6º. บรรณาธิการ Progreso.


