ระบบและตัวอย่างของ Colinear
โคลิเนียร์เวกเตอร์ เป็นเวกเตอร์ที่มีอยู่หนึ่งในสามชนิด มันเกี่ยวกับเวกเตอร์เหล่านั้นที่อยู่ในทิศทางเดียวกันหรือแนวการกระทำ นี่หมายถึงสิ่งต่อไปนี้: เวกเตอร์สองตัวหรือมากกว่านั้นจะเป็นสีผสมกันถ้าพวกมันถูกจัดเรียงเป็นเส้นตรงที่ขนานกัน.
เวกเตอร์หมายถึงปริมาณที่ใช้กับร่างกายและมีลักษณะเป็นทิศทางความรู้สึกและสเกล เวกเตอร์สามารถพบได้ในระนาบหรือในอวกาศและสามารถเป็นประเภทที่แตกต่างกัน: เวกเตอร์ colinear, เวกเตอร์พร้อมกันและเวกเตอร์ขนาน.

ดัชนี
- 1 เวกเตอร์โคลิน
- 2 ลักษณะ
- 2.1 ตัวอย่างที่ 1
- 2.2 ตัวอย่างที่ 2
- 2.3 ตัวอย่างที่ 1
- 3 ระบบเวคเตอร์ Collinear
- 3.1 Collinear vector ที่มีความรู้สึกตรงข้าม
- 3.2 เวกเตอร์คอลลิเนียด้วยความรู้สึกเดียวกัน
- 3.3 เวกเตอร์คอลลิเนียที่มีขนาดเท่ากันและมีความรู้สึกตรงกันข้าม
- 4 ความแตกต่างระหว่าง colinear และเวกเตอร์ที่เกิดขึ้นพร้อมกัน
- 5 อ้างอิง
เวกเตอร์คอลลิเนียร์
เวกเตอร์คือ collinear ถ้าแนวการกระทำของหนึ่งเป็นแนวการกระทำเดียวกันของเวกเตอร์อื่น ๆ ทั้งหมดโดยไม่คำนึงถึงขนาดและความรู้สึกของเวกเตอร์แต่ละตัว.
เวกเตอร์ใช้แทนในพื้นที่ต่าง ๆ เช่นคณิตศาสตร์ฟิสิกส์พีชคณิตและเรขาคณิตที่เวกเตอร์เป็น collinear เฉพาะเมื่อทิศทางเดียวกันโดยไม่คำนึงว่าความหมายของพวกเขาจะไม่.
คุณสมบัติ
- เวกเตอร์สองตัวหรือมากกว่านั้นเป็นเส้นตรงถ้าความสัมพันธ์ระหว่างพิกัดเท่ากัน.
ตัวอย่างที่ 1
เรามีเวกเตอร์ m = m_x; m_y และ n = n_x; n_y นี่คือ collinear ถ้า:
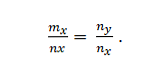
ตัวอย่างที่ 2
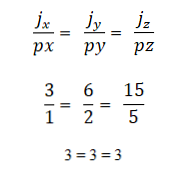
- เวกเตอร์สองตัวหรือมากกว่าเป็น collinear ถ้าการคูณผลิตภัณฑ์หรือเวกเตอร์เท่ากับศูนย์ (0) นี่เป็นเพราะในระบบพิกัดเวกเตอร์แต่ละตัวจะถูกกำหนดโดยพิกัดที่เกี่ยวข้องและถ้าหากเหล่านี้เป็นสัดส่วนกันเวกเตอร์จะเป็น collinear สิ่งนี้แสดงดังต่อไปนี้:
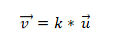
ตัวอย่างที่ 1
เรามีเวกเตอร์ a = (10, 5) และ b = (6, 3) เพื่อตรวจสอบว่าพวกเขาเป็น collinear ทฤษฎีปัจจัยถูกนำไปใช้ซึ่งจะสร้างความเท่าเทียมกันของผลิตภัณฑ์ข้าม ด้วยวิธีนี้คุณต้อง:
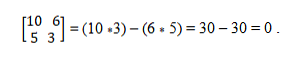
ระบบเวคเตอร์ Colinear
เวกเตอร์ colinear แสดงด้วยกราฟิกโดยใช้ทิศทางและความรู้สึกของ - พิจารณาว่าพวกเขาจะต้องผ่านจุดของการใช้งาน - และโมดูลซึ่งเป็นระดับหรือความยาวที่แน่นอน.
ระบบของคอลลิเยร์เวกเตอร์นั้นเกิดขึ้นเมื่อเวกเตอร์สองตัวหรือมากกว่านั้นทำหน้าที่กับวัตถุหรือร่างกายซึ่งเป็นตัวแทนของแรงและกระทำในทิศทางเดียวกัน.
ตัวอย่างเช่นหากมีการบังคับใช้ collinear สองครั้งบนร่างกายผลลัพธ์ของสิ่งเหล่านี้จะขึ้นอยู่กับทิศทางที่พวกมันทำเท่านั้น มีสามกรณีคือ:
เวกเตอร์คอลลิเนียร์ที่มีความรู้สึกตรงกันข้าม
ผลลัพธ์ของเวกเตอร์คอลลิเออร์สองอันเท่ากับผลรวมของสิ่งเหล่านี้:
R = Σ F = F1 + F2.
ตัวอย่าง
ถ้าสองแรงกระทำบนเกวียน F1 = 40 N และ F2 = 20 N ในทิศทางตรงกันข้าม (ดังแสดงในรูปภาพ) ผลลัพธ์คือ:
R = Σ F = (- 40 N) + 20N.
R = - 20 N.
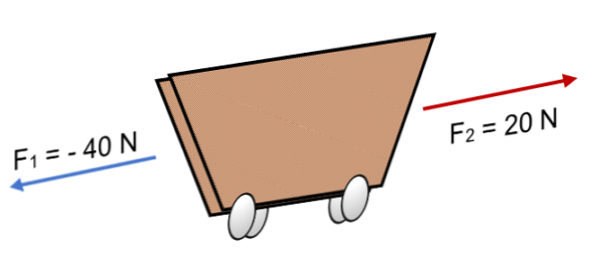
เวกเตอร์คอลลิเนียร์ด้วยความรู้สึกเดียวกัน
ขนาดของแรงลัพธ์จะเท่ากับผลรวมของคอลลิเยร์เวกเตอร์:
R = Σ F = F1 + F2.
ตัวอย่าง
ถ้าสองแรงกระทำบนเกวียน F1 = 35 N และ F2 = 55 N ในทิศทางเดียวกัน (ดังที่แสดงในภาพ) ผลลัพธ์คือ:
R = Σ F = 35 N + 55N.
R = 90 N.
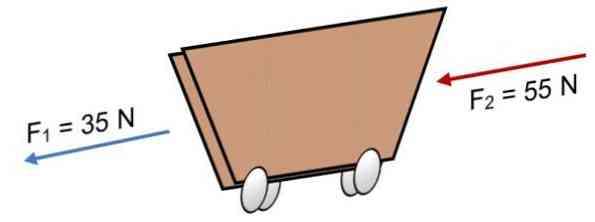
ผลบวกแสดงให้เห็นว่าเวกเตอร์คอลลิเออร์ทำหน้าที่ไปทางซ้าย.
เวกเตอร์คอลลิเนียร์ที่มีขนาดเท่ากันและมีความรู้สึกตรงกันข้าม
ผลลัพธ์ของทั้งสอง collinear vector จะเท่ากับผลรวมของ collinear vector:
R = Σ F = F1 + F2.
เนื่องจากแรงที่มีขนาดเท่ากัน แต่ในทิศทางตรงกันข้าม - นั่นคือหนึ่งจะเป็นบวกและลบอื่น ๆ - เมื่อเพิ่มแรงสองแรงผลลัพธ์จะเท่ากับศูนย์.
ตัวอย่าง
ถ้าสองแรงกระทำบนเกวียน F1 = -7 N และ F2 = 7 N ซึ่งมีขนาดเท่ากัน แต่ไปในทิศทางตรงกันข้าม (ดังที่แสดงในภาพ) ผลลัพธ์คือ:
R = Σ F = (-7 N) + 7N.
R = 0.
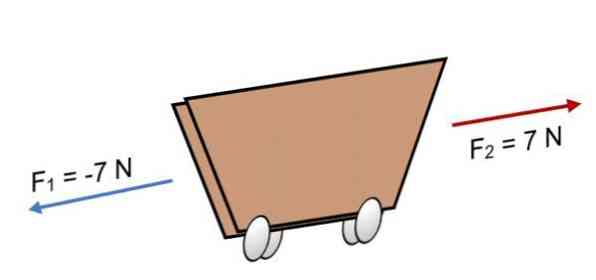
เนื่องจากผลลัพธ์มีค่าเท่ากับ 0 นั่นหมายความว่าเวกเตอร์มีความสมดุลซึ่งกันและกันและดังนั้นร่างกายจึงอยู่ในสมดุลหรือพักผ่อน (จะไม่เคลื่อนที่).
ความแตกต่างระหว่าง colinear และเวกเตอร์ที่เกิดขึ้นพร้อมกัน
เวกเตอร์คอลลิเนียร์มีลักษณะโดยมีทิศทางเดียวกันในบรรทัดเดียวกันหรือเพราะพวกมันขนานกับเส้น; นั่นคือพวกมันคือเวกเตอร์เส้นขนานโดยตรง.
ในทางตรงกันข้ามเวกเตอร์ที่เกิดขึ้นพร้อมกันนั้นถูกกำหนดเพราะมันอยู่ในแนวการกระทำต่าง ๆ ที่ถูกดักจับในจุดเดียว.
กล่าวอีกนัยหนึ่งพวกเขามีจุดกำเนิดหรือจุดกำเนิดเดียวกัน - โดยไม่คำนึงถึงโมดูลทิศทางหรือทิศทาง - สร้างมุมระหว่างพวกเขา.
ระบบของเวกเตอร์ที่เกิดขึ้นพร้อมกันนั้นถูกแก้ไขโดยวิธีทางคณิตศาสตร์หรือกราฟซึ่งเป็นวิธีของสี่เหลี่ยมด้านขนานของแรงและวิธีของรูปหลายเหลี่ยมของแรง ด้วยการพิจารณาถึงค่าของเวกเตอร์ที่เกิดขึ้นซึ่งจะระบุทิศทางที่ร่างกายจะเคลื่อนที่.
โดยพื้นฐานแล้วความแตกต่างที่สำคัญระหว่างเวกเตอร์คอลลิเนียและเวกเตอร์ที่เกิดขึ้นพร้อมกันคือแนวของการกระทำที่พวกเขาทำ: คอลลิเนียร์ที่ทำหน้าที่อยู่ในบรรทัดเดียวกัน.
นั่นคือเวกเตอร์ collinear ทำหน้าที่ในระนาบเดียว "X" หรือ "Y"; และการกระทำที่เกิดขึ้นพร้อมกันในทั้งสองระนาบเริ่มต้นจากจุดเดียวกัน.
เวกเตอร์ collinear ไม่ได้อยู่ในจุดเช่นเดียวกับเวกเตอร์ที่เกิดขึ้นพร้อมกันเพราะมันขนานกัน.
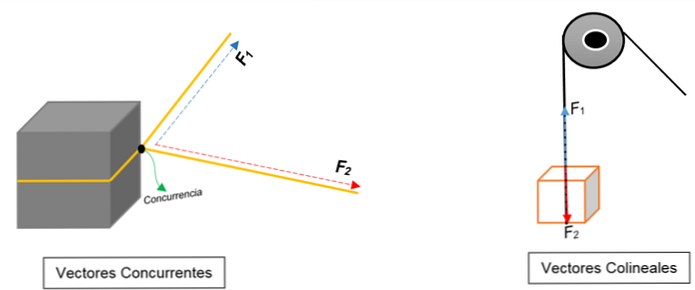
ในภาพด้านซ้ายคุณจะเห็นบล็อก มันถูกมัดด้วยเชือกและปมแบ่งออกเป็นสองส่วน เมื่อถูกดึงไปยังทิศทางที่แตกต่างกันและด้วยแรงที่แตกต่างกันบล็อกจะเคลื่อนที่ไปในทิศทางเดียวกัน.
เวกเตอร์สองตัวแสดงว่าเห็นพ้องกันในจุดหนึ่ง (บล็อก) โดยไม่คำนึงถึงโมดูลความรู้สึกหรือทิศทางของมัน.
แต่ในภาพด้านขวาจะปรากฏรอกที่ยกกล่องแทน เชือกหมายถึงแนวปฏิบัติ เมื่อมันถูกดึงออกมาแรงสองแรง (เวกเตอร์) จะกระทำกับมัน: แรงหนึ่งแรง (เมื่อปีนบล็อก) และแรงอีกอันแรงที่ออกแรงน้ำหนักของบล็อก ทั้งสองมีทิศทางเดียวกัน แต่ไปในทิศทางตรงกันข้าม ไม่เห็นด้วยในประเด็น.
การอ้างอิง
- Estalella, J. J. (1988) การวิเคราะห์เวกเตอร์ เล่มที่ 1.
- Gupta, A. (s.f. ) Tata McGraw-Hill Education.
- Jin Ho Kwak, S. H. (2015) พีชคณิตเชิงเส้น Springer Science & Business Media.
- Montiel, H. P. (2000) สาขาวิชาฟิสิกส์ 1 สาขาวิชาเทคโนโลยี กองบรรณาธิการ Patria.
- Santiago Burbano de Ercilla, C. G. (2003) ฟิสิกส์ทั่วไป บทบรรณาธิการ.
- Sinha, K. (s.f. ) หนังสือแบบเรียนคณิตศาสตร์เล่มที่ 2 เล่ม 2 สิ่งพิมพ์ Rastogi.


