สูตรการกำจัดเชิงมุมและแบบฝึกหัดที่แก้ไข

การกระจัดเชิงมุม มันถูกสร้างขึ้นเมื่อวัตถุเคลื่อนที่ตามเส้นทางหรือเส้นทางที่มีรูปร่างเป็นวงกลม มันแตกต่างจากการกำจัด ในขณะที่การกระจัดเชิงมุมวัดมุมที่เดินทาง แต่การกระจัดนั้นวัดระยะทาง.

ในการคำนวณการกระจัดเชิงมุมของวัตถุที่เคลื่อนที่ไปตามเส้นรอบวงสองวิธีสามารถใช้งานได้: หากทราบมุมเริ่มต้นและมุมสุดท้ายการกระจัดเชิงมุมจะเป็นการลบระหว่างมุมสุดท้ายและมุมเริ่มต้น.

ถ้าความยาวของการกระจัด (ความยาวของเส้นรอบวงเส้นโค้งเดินทาง) และรัศมีของเส้นรอบวงเป็นที่รู้จักแล้วการกระจัดเชิงมุมจะได้รับจากθ = l / r.

ดัชนี

• 1 สูตร
• 2 แบบฝึกหัด
  • 2.1 การออกกำลังกายครั้งแรก
  • 2.2 การออกกำลังกายครั้งที่สอง
  • 2.3 แบบฝึกหัดที่สาม
• 3 อ้างอิง

สูตร

ในการรับสูตรที่อธิบายข้างต้นคุณสามารถดูภาพต่อไปนี้:

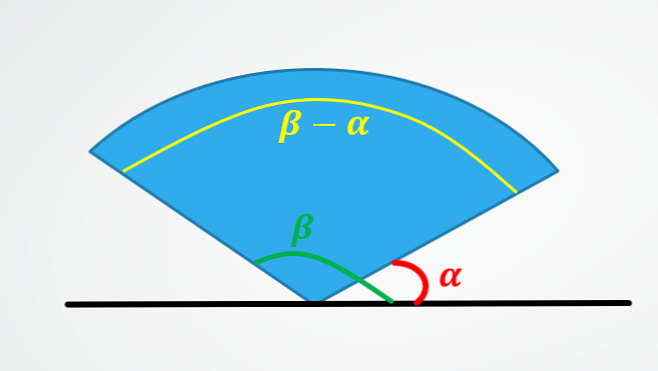
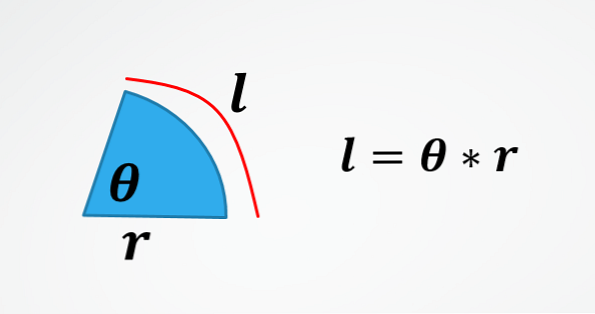
คนแรกแสดงว่าทำไมการกระจัดเชิงมุมเท่ากับการลบมุมสุดท้ายลบด้วยมุมเริ่มต้น.

ในภาพที่สองเป็นสูตรสำหรับความยาวของส่วนโค้งของวงกลม ดังนั้นโดยการลบθคุณจะได้รับสูตรที่อธิบายไว้ในตอนต้น.

การอบรม

ด้านล่างนี้เป็นแบบฝึกหัดที่ควรใช้คำจำกัดความของการกระจัดเชิงมุมและสูตรที่อธิบายไว้ข้างต้น.

การออกกำลังกายครั้งแรก

ฮวนวิ่งระยะทาง 35 เมตรบนลู่วิ่งเวียนที่มีรัศมีเท่ากับ 7 เมตร คำนวณการกระจัดเชิงมุมที่ Juan ได้ทำไว้.

ทางออก

เนื่องจากระยะทางของอาร์คเดินทางและรัศมีของเส้นรอบวงเป็นที่รู้จักกันดีจึงสามารถใช้สูตรที่สองเพื่อรู้การกระจัดเชิงมุมของ Juan การใช้สูตรที่อธิบายไว้ด้านบนคุณมีθ = 35/7 = 5 เรเดียน.

การออกกำลังกายครั้งที่สอง

หากคุณมีที่มาริโอได้เดินทางในรถของเขาครึ่งหนึ่งของการติดตามการแข่งขันแบบวงกลมการกระจัดเชิงมุมที่มาริโอได้ทำคืออะไร??

ทางออก

ในแบบฝึกหัดนี้จะใช้สูตรแรก เนื่องจากเป็นที่รู้กันว่ามาริโอได้เดินทางไปครึ่งทางแล้วจึงสามารถสันนิษฐานได้ว่าเขาเริ่มการแข่งขันในมุม 0 °และเมื่อเขามาถึงกลางวงกลมเขาได้เดินทาง 180 ° ดังนั้นคำตอบคือ 180 ° -0 ° = 180 ° = πเรเดียน.

การออกกำลังกายที่สาม

Maríaมีสระน้ำวน สุนัขของคุณวิ่งไปรอบ ๆ สระว่ายน้ำซึ่งครอบคลุมระยะทาง 18 เมตร หากรัศมีของสระว่ายน้ำเป็น 3 เมตรการกระจัดเชิงมุมทำโดยตัวนำโชคของมาเรียคืออะไร??

ทางออก

เนื่องจากสระเป็นแบบวงกลมและคุณรู้รัศมีของมันคุณสามารถใช้สูตรที่สองต่อไปได้.

เป็นที่ทราบกันว่ารัศมีมีค่าเท่ากับ 3 เมตรและระยะทางที่สัตว์เลี้ยงเดินทางนั้นเท่ากับ 18 เมตร ดังนั้นการกระจัดเชิงมุมที่ดำเนินการเท่ากับθ = 18/3 = 6 เรเดียน.

การอ้างอิง

1. Basto, J. R. (2014). คณิตศาสตร์ 3: เรขาคณิตเชิงวิเคราะห์ขั้นพื้นฐาน. กองบรรณาธิการ Patria.
2. Billstein, R. , Libeskind, S. , & Lott, J. W. (2013). คณิตศาสตร์: แนวทางการแก้ปัญหาสำหรับครูการศึกษาขั้นพื้นฐาน. López Mateos Editores.
3. Bult, B. , & Hobbs, D. (2001). ศัพท์คณิตศาสตร์ (ภาพประกอบ ed.) (F. P. Cadena, ตราด.) รุ่นที่ AKAL.
4. Callejo, I. , Aguilera, M. , Martinez, L. และ Aldea, C. (1986). คณิตศาสตร์ เรขาคณิต การปฏิรูปของวงจรบนของ E.G.B. กระทรวงศึกษาธิการ.
5. Schneider, W. , & Sappert, D. (1990). คู่มือการวาดภาพเทคนิคที่ใช้งานได้: รู้เบื้องต้นเกี่ยวกับพื้นฐานของการวาดภาพทางเทคนิคอุตสาหกรรม. Reverte.
6. โทมัส, G. บี, และฝาย, M. D. (2006). การคำนวณ: ตัวแปรหลายตัว. การศึกษาของเพียร์สัน.