วงกลมมีความสมมาตรเท่าใด
แกนสมมาตรของวงกลม พวกมันไม่มีที่สิ้นสุด แกนเหล่านี้คือแกนที่แบ่งรูปร่างทางเรขาคณิตออกเป็นสองส่วนเท่า ๆ กัน.
และวงกลมประกอบด้วยจุดทั้งหมดที่ระยะทางถึงจุดคงที่น้อยกว่าหรือเท่ากับค่าที่แน่นอน "r".
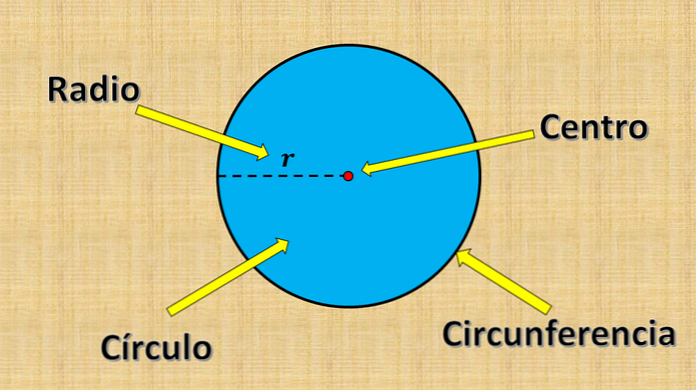
จุดคงที่ที่กล่าวถึงข้างต้นเรียกว่ากึ่งกลางและค่า "r" เรียกว่ารัศมี รัศมีเป็นระยะทางที่ยิ่งใหญ่ที่สุดที่สามารถมีได้ระหว่างจุดหนึ่งจุดบนวงกลมและศูนย์กลาง.
ในอีกทางหนึ่งส่วนของเส้นตรงใด ๆ ที่มีปลายอยู่ที่ขอบของวงกลม (เส้นรอบวง) และผ่านจุดศูนย์กลางเรียกว่าเส้นผ่านศูนย์กลาง การวัดจะเท่ากับรัศมีสองเท่าเสมอ.
วงกลมและเส้นรอบวง
อย่าสับสนกับวงกลมเป็นวงกลม เส้นรอบวงหมายถึงเฉพาะจุดที่อยู่ห่างจากจุดศูนย์กลาง "r" เท่านั้น นั่นคือเพียงขอบของวงกลม.
อย่างไรก็ตามเมื่อมองหาแกนสมมาตรมันจะไม่สนใจถ้าคุณทำงานกับวงกลมหรือเป็นวงกลม.
แกนสมมาตรคืออะไร?
แกนสมมาตรเป็นเส้นที่แบ่งออกเป็นสองส่วนเท่า ๆ กันซึ่งเป็นรูปทรงเรขาคณิตที่แน่นอน กล่าวอีกนัยหนึ่งแกนสมมาตรทำหน้าที่เหมือนกระจก.
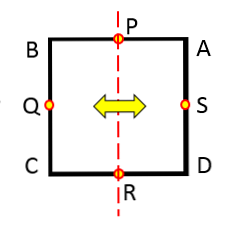
เพลาของสมมาตรของวงกลม
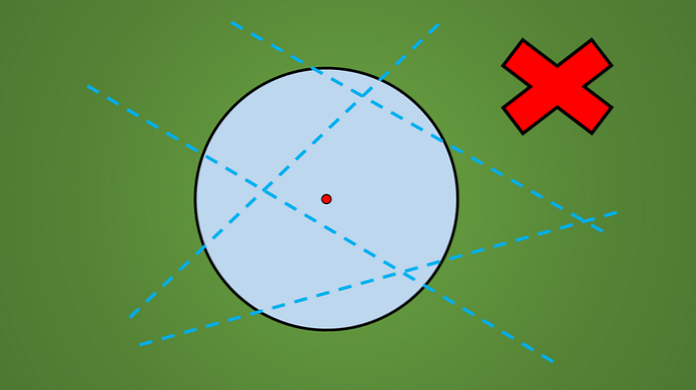
หากคุณสังเกตวงกลมใด ๆ โดยไม่คำนึงถึงรัศมีของมันคุณจะเห็นได้ว่าไม่ใช่ทุกเส้นที่ข้ามมันเป็นแกนสมมาตร.
ตัวอย่างเช่นไม่มีเส้นที่ลากในรูปภาพต่อไปนี้เป็นแกนสมมาตร.
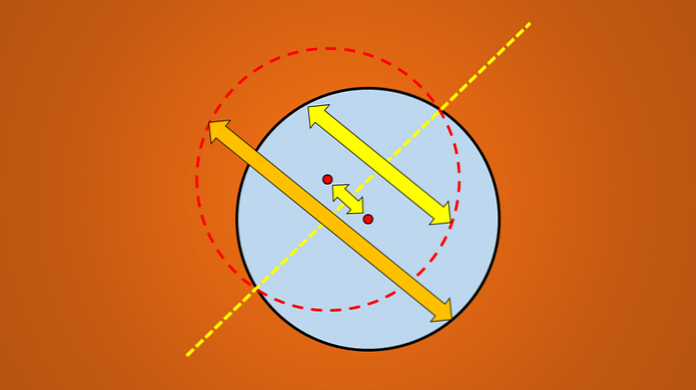
วิธีที่ง่ายในการตรวจสอบว่าเส้นเป็นแกนสมมาตรหรือไม่คือการสะท้อนรูปทรงเรขาคณิตตั้งฉากกับด้านตรงข้ามของเส้นตั้งฉาก.
หากการสะท้อนกลับไม่พอดีกับภาพต้นฉบับแสดงว่าเส้นนั้นไม่ใช่แกนสมมาตร ภาพต่อไปนี้แสดงให้เห็นถึงเทคนิคนี้.
แต่หากพิจารณาภาพต่อไปนี้เป็นที่ทราบกันดีว่าการลากเส้นเป็นแกนสมมาตรของวงกลม.
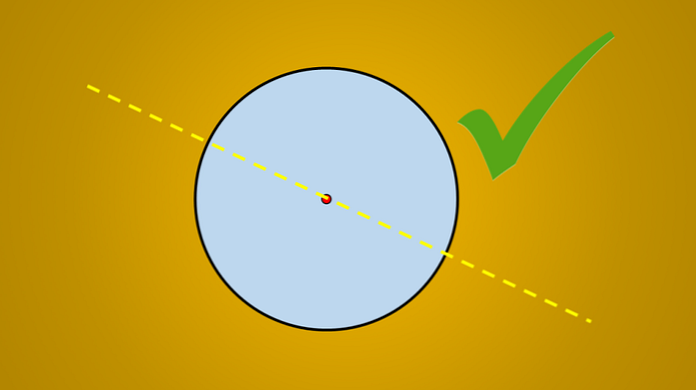
คำถามคือ: มีแกนสมมาตรมากกว่านี้ไหม? คำตอบคือใช่ หากคุณหมุนเส้นนี้ 45 องศาทวนเข็มนาฬิกาเส้นที่ได้นั้นก็จะเป็นแกนสมมาตรของวงกลม.
สิ่งเดียวกันจะเกิดขึ้นหากคุณหมุน 90 °, 30 °, 8 °และโดยทั่วไปแล้วจำนวนองศาใด ๆ.
สิ่งสำคัญเกี่ยวกับเส้นเหล่านี้ไม่ใช่ความโน้มเอียงที่พวกเขามี แต่พวกมันทั้งหมดผ่านจุดศูนย์กลางของวงกลม ดังนั้นเส้นใดก็ตามที่มีเส้นผ่านศูนย์กลางของวงกลมคือแกนสมมาตร.
ดังนั้นเนื่องจากวงกลมมีจำนวนเส้นผ่านศูนย์กลางไม่ จำกัด ดังนั้นจึงมีจำนวนแกนสมมาตรไม่ จำกัด.
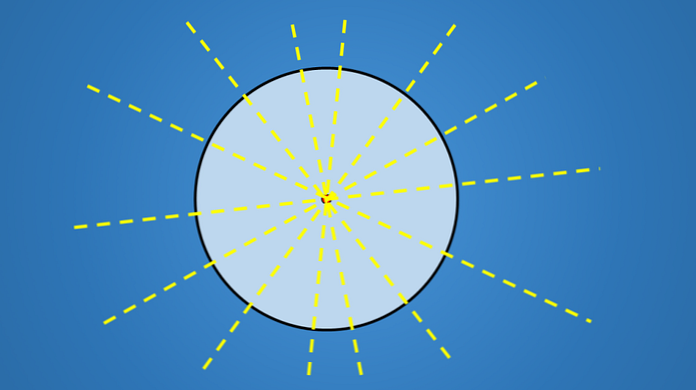
ตัวเลขทางเรขาคณิตอื่น ๆ เช่นสามเหลี่ยมรูปสี่เหลี่ยมรูปห้าเหลี่ยมรูปห้าเหลี่ยมรูปหกเหลี่ยมหรือรูปหลายเหลี่ยมอื่น ๆ มีจำนวนแกนของสมมาตร จำกัด.
เหตุผลที่วงกลมมีจำนวนแกนของสมมาตรไม่สิ้นสุดคือไม่มีด้าน.
การอ้างอิง
- Basto, J. R. (2014). คณิตศาสตร์ 3: เรขาคณิตเชิงวิเคราะห์ขั้นพื้นฐาน. กองบรรณาธิการ Patria.
- Billstein, R. , Libeskind, S. , & Lott, J. W. (2013). คณิตศาสตร์: แนวทางการแก้ปัญหาสำหรับครูการศึกษาขั้นพื้นฐาน. López Mateos Editores.
- Bult, B. , & Hobbs, D. (2001). ศัพท์คณิตศาสตร์ (ภาพประกอบ ed.) (F. P. Cadena, ตราด.) รุ่นที่ AKAL.
- Callejo, I. , Aguilera, M. , Martinez, L. และ Aldea, C. (1986). คณิตศาสตร์ เรขาคณิต การปฏิรูปของวงจรบนของ E.G.B. กระทรวงศึกษาธิการ.
- Schneider, W. , & Sappert, D. (1990). คู่มือการวาดภาพเทคนิคที่ใช้งานได้: รู้เบื้องต้นเกี่ยวกับพื้นฐานของการวาดภาพทางเทคนิคอุตสาหกรรม. Reverte.
- โทมัส, G. บี, และฝาย, M. D. (2006). การคำนวณ: ตัวแปรหลายตัว. การศึกษาของเพียร์สัน.


